Breadth-first search (BFS) is an algorithm for searching or traversing the tree or graph.BFS algorithm was invented by E.F. Moore in the late 1950s.Breadth First Search (BFS) Algorithm in detail .It is Similar to DFS Algorithm but we are using single source and traversing all possible vertices from that single source breadth wise .We have used cal_BFS() to check whether we can traverse or not . If yes print them if not just add them to the stack or queue . Remove each element from stack then check if any remaining elements is having direct path from source node. if yes print them if not add them to other stack or queue .Finally print all remaining nodes from the stack or queue.
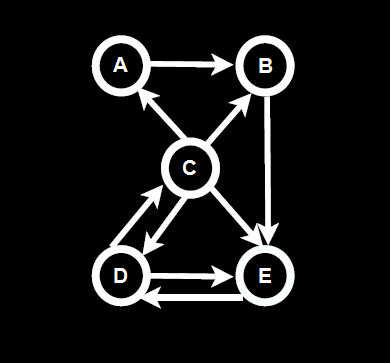
Let us take a sample example for Breadth-first Search (BFS) Algorithm.
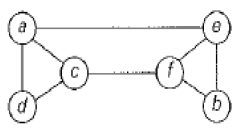
Adjacency Matrix representation:
a b c d e f
a 0 0 1 1 1 0
b 0 0 0 0 1 1
c 1 0 0 1 0 1
d 1 0 1 0 0 0
e 1 1 0 0 0 1
f 0 1 1 0 1 0
Sample Output for the above graph is :
javac BFS.java
java BFS
Enter the Number of Nodes : 6
Enter the Weights for 6 Nodes Below :
Enter the Weights for 1th row 1th Column : 0
Enter the Weights for 1th row 2th Column : 0
Enter the Weights for 1th row 3th Column : 1
Enter the Weights for 1th row 4th Column : 1
Enter the Weights for 1th row 5th Column : 1
Enter the Weights for 1th row 6th Column : 0
Enter the Weights for 2th row 1th Column : 0
Enter the Weights for 2th row 2th Column : 0
Enter the Weights for 2th row 3th Column : 0
Enter the Weights for 2th row 4th Column : 0
Enter the Weights for 2th row 5th Column : 1
Enter the Weights for 2th row 6th Column : 1
Enter the Weights for 3th row 1th Column : 1
Enter the Weights for 3th row 2th Column : 0
Enter the Weights for 3th row 3th Column : 0
Enter the Weights for 3th row 4th Column : 1
Enter the Weights for 3th row 5th Column : 0
Enter the Weights for 3th row 6th Column : 1
Enter the Weights for 4th row 1th Column : 1
Enter the Weights for 4th row 2th Column : 0
Enter the Weights for 4th row 3th Column : 1
Enter the Weights for 4th row 4th Column : 0
Enter the Weights for 4th row 5th Column : 0
Enter the Weights for 4th row 6th Column : 0
Enter the Weights for 5th row 1th Column : 1
Enter the Weights for 5th row 2th Column : 1
Enter the Weights for 5th row 3th Column : 0
Enter the Weights for 5th row 4th Column : 0
Enter the Weights for 5th row 5th Column : 0
Enter the Weights for 5th row 6th Column : 1
Enter the Weights for 6th row 1th Column : 0
Enter the Weights for 6th row 2th Column : 1
Enter the Weights for 6th row 3th Column : 1
Enter the Weights for 6th row 4th Column : 0
Enter the Weights for 6th row 5th Column : 1
Enter the Weights for 6th row 6th Column : 0
Enter the Source Vertex : 1
The Nodes that can be reachable from 1 to all other vertices are :
1 3 4 5 6 2
If you have any Comments please let me know . Enjoy Coding .
Also Read :
Let us take a sample example for Breadth-first Search (BFS) Algorithm.

import java.util.*;
public class BFS
{
public boolean visited[] = new boolean[50];
public int q[] = new int[50];
public int m[][] =new int[50][50];
public int nodes;
public void calc_BFS(int source)
{
int i,r=-1,f=0;
for(i=1;i<=nodes;i++)
if(m[source][i]>0 && !visited[i])
q[++r]=i;
if(f<=r)
{
visited[q[f]]=true;
calc_BFS(q[f++]);
}
}
public static void main(String args[])
{
int source,i,j,k=1;
int stack[]=new int[10];
int s[]=new int[10];
BFS b = new BFS();
Scanner in = new Scanner(System.in);
System.out.println("Enter the Number of Nodes \n");
b.nodes = in.nextInt();
for(i=1;i<=b.nodes;i++)
{
b.visited[i]=false;
b.q[i]=0;
}
System.out.println("Enter the Weights for \t"+b.nodes+"Nodes Below \n");
for(i=1;i<=b.nodes;i++)
for(j=1;j<=b.nodes;j++)
{
System.out.println("Enter the Weights for \t"+i+"th row \t"+j+"th Column :");
b.m[i][j] = in.nextInt();
}
System.out.println("Enter the Source Vertex :\n");
source=in.nextInt();
// Calculate the BFS
b.calc_BFS(source);
// Display nodes that are directly reachable from source
System.out.println("The Nodes that can be reachable from \t"+source+"\t to all other vertices are : \n");
for(i=1;i<=b.nodes;i++)
if(b.visited[i])
System.out.print("\t"+i+"\t");
else
{
stack[k++]=i;
}
// pop out the remaining elements from the stack which are directly reachable from source
k=k-1;j=1;
int ele,f=0;
while(k>0)
{
//get element from stack and check if there is any direct path from source to that element
ele=stack[k--];
for(i=1;i<=b.nodes;i++)
{
if(ele==i && b.m[1][i]==1)
{
System.out.print("\t"+ele+"\t");
f=1;
break;
}
else
f=0;
}
// if no direct path from source ,collect them and store it in array S .
if(f==0)
s[j++]=ele;
}
k=j-1;
j=1;
// pop out the remaining elements from the stack even though they are not reachable directly from source
while(j<=k)
{
System.out.print("\t"+s[j++]+"\t");
}
}
}
Adjacency Matrix representation:
a b c d e f
a 0 0 1 1 1 0
b 0 0 0 0 1 1
c 1 0 0 1 0 1
d 1 0 1 0 0 0
e 1 1 0 0 0 1
f 0 1 1 0 1 0
Sample Output for the above graph is :
javac BFS.java
java BFS
Enter the Number of Nodes : 6
Enter the Weights for 6 Nodes Below :
Enter the Weights for 1th row 1th Column : 0
Enter the Weights for 1th row 2th Column : 0
Enter the Weights for 1th row 3th Column : 1
Enter the Weights for 1th row 4th Column : 1
Enter the Weights for 1th row 5th Column : 1
Enter the Weights for 1th row 6th Column : 0
Enter the Weights for 2th row 1th Column : 0
Enter the Weights for 2th row 2th Column : 0
Enter the Weights for 2th row 3th Column : 0
Enter the Weights for 2th row 4th Column : 0
Enter the Weights for 2th row 5th Column : 1
Enter the Weights for 2th row 6th Column : 1
Enter the Weights for 3th row 1th Column : 1
Enter the Weights for 3th row 2th Column : 0
Enter the Weights for 3th row 3th Column : 0
Enter the Weights for 3th row 4th Column : 1
Enter the Weights for 3th row 5th Column : 0
Enter the Weights for 3th row 6th Column : 1
Enter the Weights for 4th row 1th Column : 1
Enter the Weights for 4th row 2th Column : 0
Enter the Weights for 4th row 3th Column : 1
Enter the Weights for 4th row 4th Column : 0
Enter the Weights for 4th row 5th Column : 0
Enter the Weights for 4th row 6th Column : 0
Enter the Weights for 5th row 1th Column : 1
Enter the Weights for 5th row 2th Column : 1
Enter the Weights for 5th row 3th Column : 0
Enter the Weights for 5th row 4th Column : 0
Enter the Weights for 5th row 5th Column : 0
Enter the Weights for 5th row 6th Column : 1
Enter the Weights for 6th row 1th Column : 0
Enter the Weights for 6th row 2th Column : 1
Enter the Weights for 6th row 3th Column : 1
Enter the Weights for 6th row 4th Column : 0
Enter the Weights for 6th row 5th Column : 1
Enter the Weights for 6th row 6th Column : 0
Enter the Source Vertex : 1
The Nodes that can be reachable from 1 to all other vertices are :
1 3 4 5 6 2
If you have any Comments please let me know . Enjoy Coding .
Also Read :